Dies und das - Kräfte am Spinnrad

Warum wird die Einzugskraft mit vollerwerdender Spule kleiner?

Ausgangsbedingungen

Betrachten wir ein einfädiges, spulengetriebenes Spinnrad.
Ein Faden wurde gerade eben ausgezogen. Jetzt wird er zwischen Daumen und Zeigefinger festgehalten. Die Spule rotiert gleichmäßig und langsam, der Flügel ist über den Faden mit der Spule verbunden und rotiert daher mit der gleichen Winkelgeschwindigkeit wie die Spule. Der Luftwiederstand des Flügels wird wegen seiner geringen Geschwindigkeit vernachsässigt.
Der Faden wird verdrallt.

Feststellung:
Die einziehende Kraft des Fadens am Einzugsloch wird mit größer werdendem Spulendurchmesser kleiner.

Fragen:
Welchen Zusammenhang gibt es zwischen Einzugskraft und Spulenbremse bei vollerwerdender Spule?
Müssen die Füße mehr Kraft aufbringen?

Das Drehmoment der Spule

Das große Schwungrad, angetrieben durch das Treten mit einem Fuß oder beiden Füßen, rotiert gleichmäßig.
Über ein offenes Riemengetriebe wird die Kraft auf den Wirtel übertragen. Die Formeln dafür sind, wie so oft, komlizierter als man sie sich wünschen würde. Wir nehmen an, die antreibende Kraft wird reibungslos auf den Wirtel übertragen.
Auf den Wirtel wird also die antreibende Kraft F_a übertragen. Da wir uns in einem rotierenden System befinden, wirkt auf den Wirtel auch ein Drehmoment M. Das Drehmoment ist definiert als Kraft mal Hebelarm. Da Kraft und Hebelarm nicht parallel wirken, sondern in einem Winkel zueinander stehen, ist das Drehmoment eine vektorielle Größe. Es gilt allgemein:

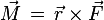
Das Drehmoment wird bei Wikipedia erläutert: de.wikipedia.org/wiki/Drehmoment

Wir betrachten unser Spinnrad zwischen Wirtel und Einzugsöffnung als abgeschlossenes System im Gleichgewichtszustand.

Auf den Wirtel wirkt das Drehmoment M_w = F_a · r_w (r_w ... Radius des Wirtels)
Da der Wirtel mit der Spule starr verbunden ist, wirkt auf die Spule an der Stelle des abgehenden Fadens das selbe Drehmoment M_w = M_spule = konstant

Demzufolge gilt: F_a · r_w = F_spule · r_spule
mit
F_spule ... auf den Faden wirkende Kraft zwischen Haken und Spule
r_spule ... der aktuelle Radius der Spulenwicklung

Nach Umstellung:
F_spule = F_a · r_w / r_spule

Schlussfolgerung:
Die Kraft auf den Faden gleich hinter der Spule bei gleichbleibender Tretkraft ist also umgekehrt proportional zur Dicke der Wicklung, d. h. sie wird im gleichen Verhältnis kleiner je dicker die Spule wird.

Nun teilt sich die auf den Faden an der Spule wirkende Kraft F_spule nach der Umlenkung des Fadens am Flügelhaken in zwei Kräfte auf:
- F_e .... die Fraft, die weiter längs des Fadens bis zum Einzugsloch wirkt und in
- F_fl ... die Antriebskraft des Flügels

Beider wirkende Kräfte treten zwei gleichgroße Gegenkräfte entgegen.
Das ist für F_e die haltende Kraft der Finger und
für F_fl die Reibungskraft an der Flügelbremse und weitere Verluste, wie den durch den Luftwiderstand ervorgerufenen.
Leichtfertig ließe sich annehmen, es gelte die einfach zu überschauende Summe:
F_spule = F_e + F_fl
Das ist jedoch leider falsch.
Die Gleichung wäre richtig, verliefen die Kräfte F_e und F_fl in die selbe Richtung.
Da F_spule längs des Fadens und F_fl senkrecht zur Flügelachse wirkt, muss das Kräftegleichgewicht vektoriell angesetzt werden.
Zur Veranschaulichung der wirkenden Kräfte dient die folgende Darstellung einer noch leeren Henkys-Spule.

Kräfte an der leeren Henkysspule

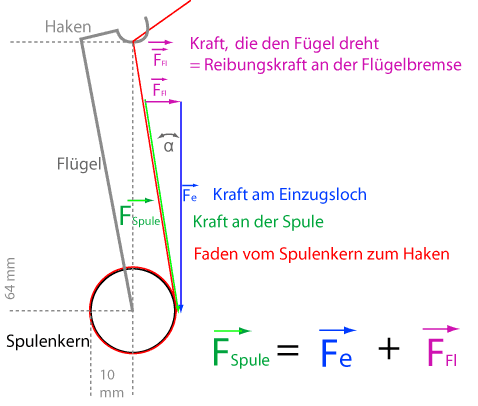
F_fl ist die Reibungskraft der Flügelbremse. Da sie in unserer Betrachtung nicht verändert wird, ist sie eine Konstante. Für die gesuchte Einzugskraft F_e ergibt sich:

F_e = F_spule · cos α

Oben wurde bereits festgestellt:
F_spule = F_a · r_w / r_spule

Daraus ergibt sich für die Einzugskraft ein gerundeter Wert:

F_e ≈ F_a · r_w / r_spule · cos α

Bei leere Spule ist der Winkel ca. 10°, sein Kosinus nahe eins und damit der Einfluss gegenüber der Einzugskraft zu vernachlässigen. Es gilt daher:
F_e ≈ F_a · r_w / r_spule
Ergebnis:
Die einziehende Kraft ist bei leerer Spule umgekehrt proportional zur Dicke des Spulenkerns, dh. sie ist größer je dünner er ist.

Bei sich füllender Spule ist der Winkel des Fadens (von der Spule zum Haken) den er gegen die Senkrechte bildet nicht mehr zu vernachlässigen.
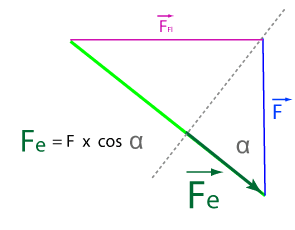
Wie sich der Winkel alpha bei voller Spule auswirkt, zeigt die folgende maßstabgerechte Studie:

Kräfte an der vollen Henkysspule

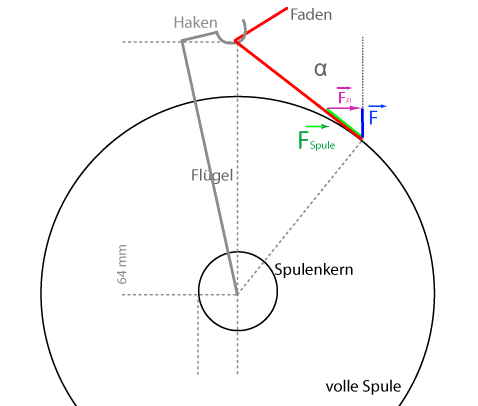
Da an der Flügelbremse nicht gedreht wurde, ist F_fl unverändert zur leeren Spule.
Der violette Kraftvektor kann daher mit gleicher Länge parallel wie oben eingetragen werden.
Aus F_fl ergeben sich die beiden fehlenden Kraftvektoren (grün und blau).
Die blaue Kraft F ist gegenüber der leeren Spule um ein vielfaches kleiner geworden.
Die eingezeichnete resultierende blaue Kraft ist allerdings noch nicht die gesuchte Einzugskraft.
Die Einzugskraft wirkt längs des Fadens, die blaue Kraft F parallel zur Senkrechten.

Es kann vorerst festgestellt werden, die einziehende Kraft verringert sich überproportional stark mit wachsender Spulendicke.
Es ist zu erkennen, dass hierfür der größerwerdende Winkel alpha verantwortlich ist.

Alpha ist keine Unbekannte

Der Winkel des Fadens zur Senkrechten wird bestimmt vom festen Abstand des Hakens vom Drehmittelpunkt und vom veränderlichen Spulenradius. Er kann über den Sinus ermittelt werden. Die folgende Skizze zeigt den Zusammenhang an der vollen Spule.

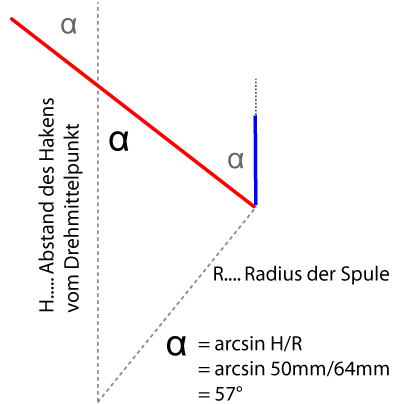
Es wird langsam kompliziert

Die Einzugskraft wird also kleiner weil die Spule dicker wird:
F_a · r_w = F_spule · r_spule
und weiterhin wird sie kleiner weil der Winkel des Fadens größer wird.

Die Einzugskraft wirkt längs des Fadens

Nur der Teil des blauen Kraftvektors F der längs des Fadens wirkt, wirkt als Einzugskraft.

Die Einzugskraft in Abhängigkeit von Flügelbremse und Spulendicke

Nach den Skizzen lassen sich die Gleichungen aufstellen:

F_e = F · cos alpha
F = F_spule · cos alpha
alpha = arcsin r_spule/H
F_spule = F_fl / sin alpha

Aus ihnen lässt sich durch Einsetzung der gesuchte Zusammenhang für die Einzugskraft aufstellen:

F_e = F_fl · cos alpha / tan alpha
mit
alpha = arcsin r_spule/H

Die Einzugskraft lässt sich berechnen aus lediglich der Bremskraft der Spulenbremse, dem Radius der aktuellen Spulenwicklung und dem festen Abstand des Flügelhakens von der Drehachse.

Welchen Einfluss hat die Antriebskraft?

Die Antriebskraft F_a war die Kraft, die von den Füßen über den Keilriemen auf den Wirtel übertragen wird.
Oben wurde festgestellt:
F_a · r_w = F_spule · r_spule

Der Sinus eines Winkels ist im rechtwinkeligen Dreieck definiert als Gegenkathete durch Hypotenuse.
Es gilt:
sin alpha = r_spule / H, siehe Absatz 'Alpha ist keine Unbekannte'
weiterhin gilt auch:
sin alpha = F_fl / F_spule, nach Absatz 'Kräfte an der vollen Henkysspule'
Durch Gleichsetzung gilt:
F_fl / F_spule = r_spule / H
Nach Umstellung und Einsetzung ergibt sich aus beiden Gleichungen:

F_a = F_fl · H / r_w

Die Antriebskraft hängt nur von der Flügelbremse und von den festen Größen Radius des Wirtels und Abstand des Hakens von der Drehachse ab.
Sie ist nicht abhängig vom Füllstand der Spule.

Erläuterung zum Diagramm rechts

Das Diagramm zeigt die Abnahme der Einzugskraft mit vollerwerdender Spule.
Jede der drei Kurven wurde für eine Bremskraft der Flügelbremse mittels Javascript berechnet.
Die kleinste Bremskraft wurde experimentell ermittelt. Dabei wurde festgestellt, bei welcher Kraft sich der Flügel ohne angelegter Bremse zu drehen beginnt (Losbrechkraft). Bei horizontalgestelltem Flügel habe ich dazu Gewicht an den Haken gehängt und es anschließend gewogen.
Die Messmethode ist sehr ungenau und ermittelt nur die Größenordnung der Bremskraft der Flügelbremse. Bei genauerer Messung müsste berücksichtigt werden, dass die Gleitreibungskraft jenseits der Haftgrenze kleiner als die Losbrechkraft ist. Den Vorgang habe ich mit angezogener Bremse wiederholt.

Berechne die Kräfte deines Spinnrades

Gehe auf die Seite 'Berechnungen zur Einzugskraft'
und gib deine Werte ein.

Jörg

zurück
nach oben